Annotated Ideal Harmonic Transformer Math Manipulative

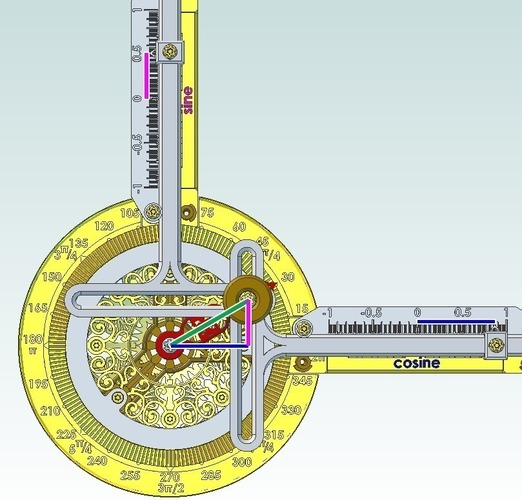
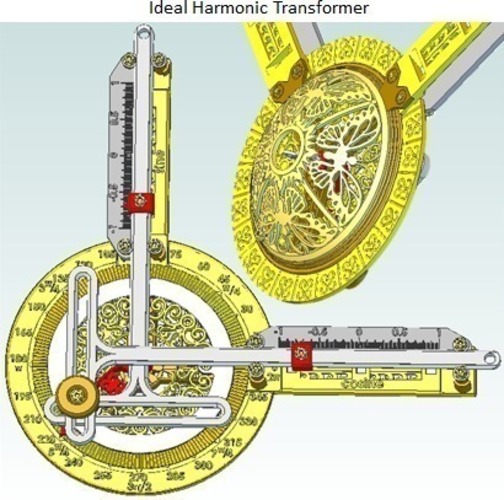
SummaryTreat yourself and your classroom to a machine that shows you how Sine and Cosine relate to angles. There is an animation on my blog: http://swampcastle.blogspot.com/2013/11/harmonic-transformer-for-classroom.html I have also imported and assembled the models into OnShape, where you can take it for a virtual spin. Try it out; you won't be disappointed. About Onshape: http://swampcastle.blogspot.com/2015/08/onshape-shapes-up-great.html Link to the model: https://cad.onshape.com/documents/5c003295166a40c699e9ca02/w/8ec0747e1c854c81bd8468e9/e/b660adf4fde44b19baf860fa How to use: Use the knob to rotate the arm to an angle. Read the value on the Sine and Cosine scales. Sine and Cosine values are given for a circle with a radius of 1, which is also called a "unit" circle. To obtain lengths for a circle with a radius other than one, multiply the reading from the machine by the desired radius. Sine and cosine are trigonometric functions of an angle, defined by using right triangles. In one of the figures, a right triangle has been drawn on top of the Harmonic Transformer. The angle is set to 30 degrees. The hypotenuse is the radius of the circle, shown as a green line. The radius is drawn from the arm's pivot center to the center of the knob, where the pin is. The blue horizontal line is the "adjacent" side of the triangle, and the magenta vertical line is the "opposite" side. Notice that the blue side is the same length as the reading on the cosine scale. Similarly, the magenta side is the same length as the reading on the sine scale.InstructionsAssembly instructions are provided with pictures and details at my blog: http://swampcastle.blogspot.com/2013/11/harmonic-transformer-for-classroom.html This is essentially my original Ideal Harmonic Transformer, with the addition of more labels. The labels make it easier to use, and are easier to read because the text is raised instead of cut-in.